그래프

📍 용어

  • 정점(Vertex): 그래프의 노드 또는 점
  • 간선(Edge): 정점 간의 연결. 부모-자식 개념 없음 
  • 가중치(Weight): 간선(엣지)에 할당된 값으로, 주로 두 노드(정점) 간의 관계의 강도, 비용, 거리 등을 나타냄
  • 차수(Degree): 정점에 연결된 간선의 수
  • 진입 차수: 방향 그래프에서 특정 정점으로 들어오는 간선의 수
  • 진출 차수: 방향 그래프에서 특정 정점에서 나가는 간선의 수
  • 경로(Path): 그래프의 두 정점 간에 존재하는 간선의 연속
  • 사이클(Cycle): 시작 정점에서 출발하여 다시 시작 정점으로 돌아오는 경로. 트리와 가장 큰 차이
  • 연결 그래프: 모든 정점이 서로 연결된 그래프
  • 포화그래프: V 개의 정점을 가지는그래프는 최대 V *(V–1)/ 2 간선이 가능
    • ex) 4개 정점이 있는 그래프의 최대 간선 수는 (4*3/2) = 6개
  • 부분 그래프(Subgraph): 원래 그래프의 일부 정점과 간선으로 구성된 그래프
  • 방향 그래프: 간선에 방향이 있는 그래프. 예를 들어, A ➡️ B는 A에서 B로 가는 방향을 의미
  • 무방향 그래프: 간선에 방향이 없는 그래프. A와 B 간의 관계는 양방향으로 해석

 

📍 그래프를 사용하는 예

1. 소셜 네트워크: 사람(정점)과 사람 간의 친구 관계(간선)를 나타내는 그래프

2. 도로망: 도로의 교차점(정점)과 도로(간선)를 표현하는 그래프

3. 웹 페이지: 웹 페이지(정점)와 링크(간선) 간의 관계를 나타내는 그래프

 

 

👩🏻‍💻 구현해보기

  • 인접행렬로 저장한 그래프
/*
	첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 
	둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 
	같은 간선은 한 번만 주어진다.
	
	6 5
	1 2
	2 5
	5 1
	3 4
	4 6
*/

package graph;

import java.util.Scanner;

public class 인접행렬 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int N = sc.nextInt();
		int M = sc.nextInt();

		int[][] adjM = new int[N + 1][N + 1]; // 1부터 N까지 사용하므로

		for (int i = 0; i < M; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();

			// 무방향 그래프의 경우 양쪽 모두에 1을 설정
			adjM[u][v] = 1;
			adjM[v][u] = 1;
		}
		
		// 인접 행렬 출력 (디버깅 용도)
        System.out.println("인접 행렬:");
        
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                System.out.print(adjM[i][j] + " ");
            }
            System.out.println();
        }
        
        sc.close();
	}

}
  • 인접리스트로 저장한 그래프
/*
	첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 
	둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 
	같은 간선은 한 번만 주어진다.
	
	6 5
	1 2
	2 5
	5 1
	3 4
	4 6
*/

package graph;

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class 인접리스트 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int N = sc.nextInt();
		int M = sc.nextInt();

		List<List<Integer>> adjL = new ArrayList<>(N + 1);

		for (int i = 0; i <= N; i++) {
			adjL.add(new ArrayList<>());
		}
		
		for(int i = 0; i < M; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();

			// 무방향 그래프의 경우 양쪽 리스트에 추가
			adjL.get(u).add(v);
			adjL.get(v).add(u);
			
		}
		
		// 인접 리스트 출력 (디버깅 용도)
        System.out.println("인접 리스트");
        
        for (int i = 1; i <= N; i++) {
            System.out.print(i + ": "); // 정점 번호 출력
            for (int neighbor : adjL.get(i)) {
                System.out.print(neighbor + " "); // 인접한 정점 출력
            }
            System.out.println();
        }
        
        sc.close();
	}

}

 

그래프를 탐색하는 방법

1. DFS(깊이 우선 탐색)

출처: https://sethuram52001.medium.com/data-structures-and-algorithms-undirected-graph-processing-491d4fdefad0
출처: https://hwan001.co.kr/146

  • DFS 인접행렬 구현
/*
	정점수
	간선수
	탐색시작노드
	간선수만큼 연결정보
	
	5
	5
	1
	1 2
	1 5
	2 3
	2 4
	3 4
    
	출력: 1 2 3 4 5
*/

package graph;

import java.util.Scanner;

public class DFS_인접행렬탐색 {
	static int[][] arr;
	static boolean[] isSelected;
	static StringBuilder sb = new StringBuilder();
	static int V;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		V = sc.nextInt();
		int E = sc.nextInt();
		int start = sc.nextInt();

		arr = new int[V + 1][V + 1];

		for (int i = 0; i < E; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
            
			arr[u][v] = arr[v][u] = 1;
		}

		isSelected = new boolean[V + 1];
		
		dfs(start);
        
		System.out.println(sb);
		sc.close();

	}
	
	static void dfs(int curV) {
		isSelected[curV] = true;
		sb.append(curV).append(" ");
		
		for(int toV = 1; toV <= V; toV++) {
			if(!isSelected[toV] && arr[curV][toV] != 0 ) {
				dfs(toV);
			}
		}
	}

}
  • DFS 인접리스트 구현
/*
	정점수
	간선수
	탐색시작노드
	간선수만큼 연결정보
	
	5
	5
	1
	1 2
	1 5
	2 3
	2 4
	3 4
	
	출력: 1 2 3 4 5
*/

package graph;

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class DFS_인접리스트탐색 {
	static List<List<Integer>> list = new ArrayList<>();
	static boolean[] isSelected;
	static StringBuilder sb = new StringBuilder();
	static int n;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		n = sc.nextInt();
		int m = sc.nextInt();
		int start = sc.nextInt();

		for (int i = 0; i <= n; i++) {
			list.add(new ArrayList<>());
		}
		
		for(int i = 0; i < m; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			
			list.get(u).add(v);
			list.get(v).add(u);
		}
		
		isSelected = new boolean[n + 1];
		
		dfs(start);
        
		System.out.println(sb);
		sc.close();

	}
	
	static void dfs(int cur) {
		isSelected[cur] = true;
		sb.append(cur).append(" ");
		
		for(int i : list.get(cur)) { // 갈 수 있는 곳들만 뽑음
			if(!isSelected[i]) {
				dfs(i);
			}
		}
	}

}

 

2. BFS(너비 우선 탐색)

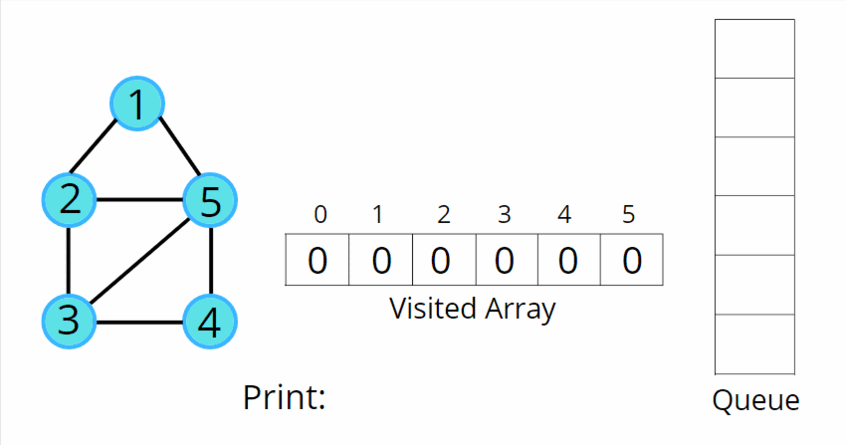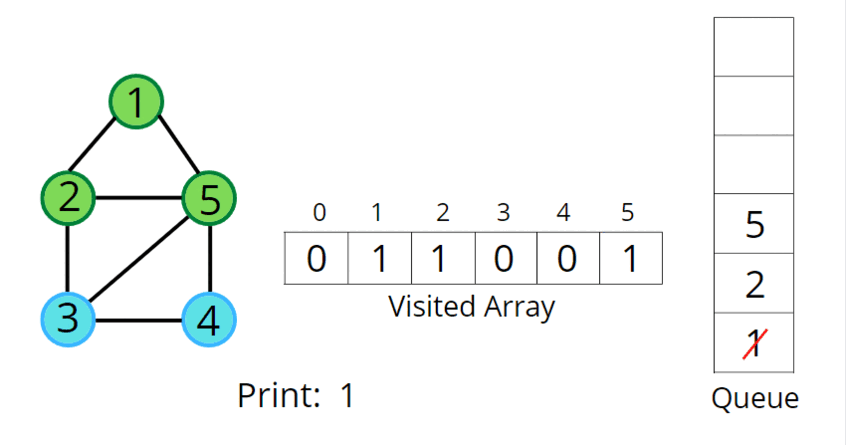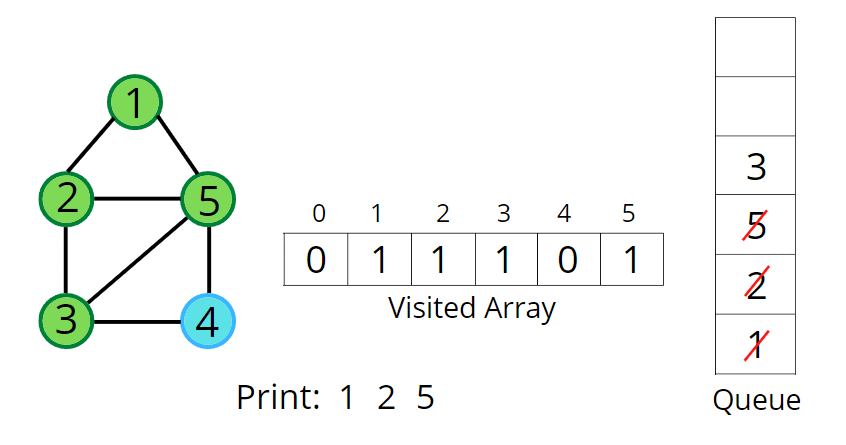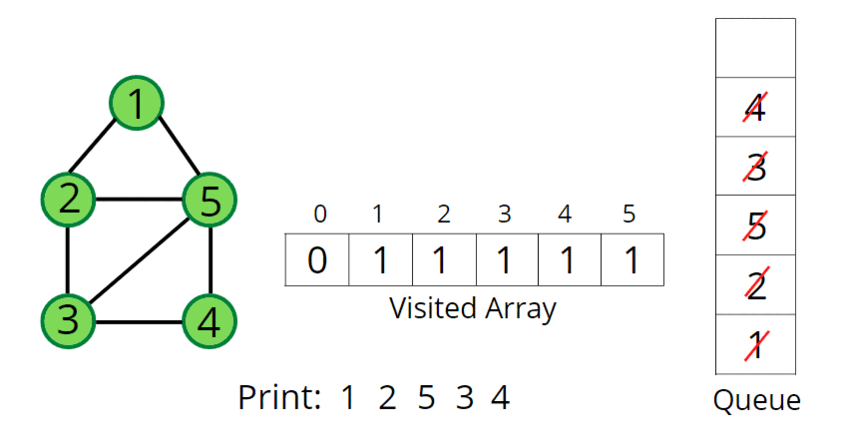
출처: https://takeuforward.org/graph/breadth-first-search-bfs-level-order-traversal/

  • BFS 인접행렬 구현
/*
	정점수
	간선수
	탐색시작노드
	간선수만큼 연결정보
	
	5
	5
	1
	1 2
	1 5
	2 3
	2 4
	3 4
	
	출력: 1 2 5 3 4
*/

package graph;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class BFS_인접행렬탐색 {
	static int[][] arr;
	static boolean[] isSelected;
	static StringBuilder sb = new StringBuilder();
	static int V;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		V = sc.nextInt();
		int E = sc.nextInt();
		int start = sc.nextInt();

		arr = new int[V + 1][V + 1];

		for (int i = 0; i < E; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();

			arr[u][v] = arr[v][u] = 1;
		}
		
		isSelected = new boolean[V + 1];
		
		// 1. Queue 만들기
		Queue<Integer> q = new LinkedList<>();

		// 2. q에 start node 넣기
		q.offer(start);
		
		// 3. 방문 체크
		isSelected[start] = true;
		
		// 4. q에서 데이터 꺼내 처리
		while(!q.isEmpty()) {
			int curV = q.poll();
			// 5. 하고 싶은 일 수행
			sb.append(curV).append(" ");
			
			for (int i = 1; i <= V; i++) {
				if(!isSelected[i] && arr[curV][i] != 0) {
					// 6. 갈 수 있는 새 정점을 q에 넣기
					q.offer(i);
					isSelected[i] = true;
				}
			}
		}
	
		System.out.println(sb);
		sc.close();

	}
}
  • BFS 인접리스트 구현
/*
	정점수
	간선수
	탐색시작노드
	간선수만큼 연결정보
	
	5
	5
	1
	1 2
	1 5
	2 3
	2 4
	3 4
	
	출력: 1 2 5 3 4
*/

package graph;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;

public class BFS_인접리스트탐색 {
	static List<List<Integer>> list = new ArrayList<>();
	static boolean[] isSelected;
	static StringBuilder sb = new StringBuilder();
	static int V;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		V = sc.nextInt();
		int E = sc.nextInt();
		int start = sc.nextInt();

		for (int i = 0; i <= V; i++) {
			list.add(new ArrayList<>());
		}
		

		for (int i = 0; i < E; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			
			list.get(u).add(v);
			list.get(v).add(u);
		}

		isSelected = new boolean[V + 1];
		
		Queue<Integer> q = new LinkedList<>();
		
		q.offer(start);
		isSelected[start] = true;
		
		while(!q.isEmpty()) {
			int curV = q.poll();
			sb.append(curV).append(" ");
			
			for(int i : list.get(curV)) {
				if(!isSelected[i]) {
					q.offer(i);
					isSelected[i] = true;
				}
			}
			
		}
		
		System.out.println(sb);
		sc.close();

	}

}

 

👩🏻‍💻 문제 풀어보기: 백준_DFS와 BSF_1260

package graph;

import java.util.*;

public class 백준_DFS와BFS_1260 {
	static List<List<Integer>> list = new ArrayList<>();
	static boolean[] isSelected;
	static StringBuilder sb = new StringBuilder();
	static int n;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		n = sc.nextInt();
		int m = sc.nextInt();
		int start = sc.nextInt();

		for (int i = 0; i <= n; i++) {
			list.add(new ArrayList<>());
		}
		
		for(int i = 0; i < m; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			
			list.get(u).add(v);
			list.get(v).add(u);
		}
		
		// 각 정점의 연결 리스트를 정렬 (오름차순 방문을 위함)
        for (int i = 1; i <= n; i++) {
            Collections.sort(list.get(i));
        }
		
		isSelected = new boolean[n + 1];
		dfs(start);
        
		sb.append("\n");
        
        isSelected = new boolean[n + 1];
        bfs(start);
        
		System.out.println(sb);
		sc.close();

	}
	
	static void dfs(int cur) {
		isSelected[cur] = true;
		sb.append(cur).append(" ");
		
		for(int i : list.get(cur)) { // 갈 수 있는 곳들만 뽑음
			if(!isSelected[i]) {
				dfs(i);
			}
		}
	}
    
    static void bfs(int start) {
        Queue<Integer> q = new LinkedList<>();
		
		q.offer(start);
		isSelected[start] = true;
		
		while(!q.isEmpty()) {
			int curV = q.poll();
			sb.append(curV).append(" ");
			
			for(int i : list.get(curV)) {
				if(!isSelected[i]) {
					q.offer(i);
					isSelected[i] = true;
				}
			}
			
		}
    }
}
728x90
반응형

'LG 유플러스 유레카 SW > Algorithm' 카테고리의 다른 글

[#21] MST(최소신장트리) + 다익스트라 알고리즘  (1) 2025.02.24
[#20] 알고리즘 - 최단 경로  (0) 2025.02.21
[#18] 비선형 자료구조 - 트리  (0) 2025.02.19
[#17] 순열 & 조합 & 부분집합  (0) 2025.02.18
[#16] 알고리즘 - 정렬  (0) 2025.02.17

티스토리툴바